Существуют стандартные критерии определения выбросов в выборке при заданном уровне значимости/доверия. Примерами таких критериев служат: критерий Шовене, тест Граббса, критерий Пирса, Q-тест Диксона. Упомянутые критерии (за исключением критерия Граббса) выстраивают выборку по возрастанию и проверяют крайние значения (min, max элемент выборки) на выброс, подключается таблица критических значений.
Содержание
Значения в таблицах зависят от количества элементов в выборке и уровня доверия/значимости. Критерии позволяют определить точно один выброс, в случае, когда их много, критерии могут не работать.
Критерий Граббса позволяет находить несколько выбросов (1, 2 ,3 можно расширить до n), но основное предположение этого критерия, это нормальное распределение данных, что очень сильно ограничивает возможность применения данного критерия к автоматической обработки данных.
Описание подхода
1. Выстраиваем все элементы выборки по возрастанию (от меньшего к большему):
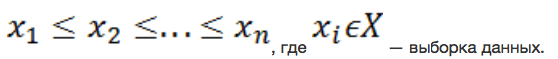
В случае многомерной выборки для сравнения элементов предлагается рассматривать евклидову метрику.
2. Определение максимально возможный процент выбросов в выборке (указывается экспертом, например 5%)
Здесь определяется верхняя граница количества выбросов. Это не значит, что число выбросов будет составлять строго 5% от выборки, это число будет меньше либо равно 5%. Этот параметр обозначим за g.
3. Строим ряд разностей
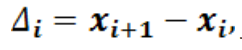
таким образом получим n-1 положительных элементов в последовательности (последовательность не обязательно возрастающая):
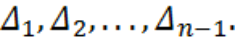
4. Находим максимальную разность
В последовательности разностей находим максимальную разность: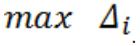 
5. Проверка, попадает ли выброс в заданную в п.2. область
В п.4. получили некоторый индекс i', который является максимальным в последовательности разностей. Если этот индекс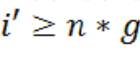 
и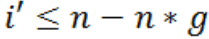 
в то же время, то в выборке нет выбросов, прекращаем проверку.
В противном случае, элемент с индексом i'подозрителен на выброс.
Если индекс попал в интервал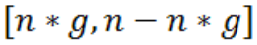 
это значит, что максимальная разность достигнута в середине выборки, где предположили, что выбросов нет, задав параметр g.
6. Вырезаем подвыборку из начального набора данных
Здесь имеем два случая:
7. Среднее значение разностей
Находим среднее значение выборки разностей (п.3.) с учетом набора индексов (п.6.):
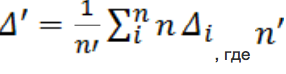– число элементов в вырезанной подвыборке.
8. Среднеквадратическое отклонение
Рассчитываем характеристику разброса элементов:
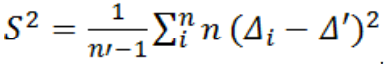
9. Считаем статистику Граббса
Используем формулу Граббса для расчета значения статистики:
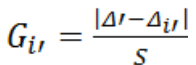
10. Задаем уровень значимости
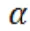– величина вероятности ошибки ( обычно 1%, 5%, 10%).11. Использование таблицы критических значений, сравнение величины статистики из п.9. с критическим значением
По значению уровня значимости и числу элементов в подвыборке n' находим критическое значение в таблице Граббса, обозначим его за
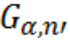
Сравниваем полученное значение полученное в п.9. Возможны два случая:
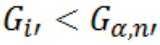– исследуемое значение не является выбросом и в выборке нет начальном наборе данных нет выбросов вообще.
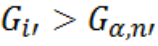– исследуемое значение является выбросом.
Если оно находится во второй половине выборки (п.1.), то все значения идущие после i' являются выбросами, если оно находится в первой половине выборки (п.1.), то все значения идущие до i' являются выбросами.
12. Если в п.11. был обнаружен выброс, то из начальной выборки убираем выбросы и повторяем весь алгоритм с первого пункта (п.1.)
Если вы уже используете сервис КОРУС | Управление запасами, но у вас остались вопросы по настройке интерфейса и отчетов, напишите нам на wms@korusconsuting.ru.
Вы можете ознакомиться с функциональностью сервиса и оценить его эффективность на примере собственных данных.
Запросите бесплатный тестовый доступ к сервису и начните оптимизацию запасов прямо сейчас!
Задайте вопрос эксперту на нашем сайте или по телефону: +7 495 130 01 87.
